حدسية غولدباخ
حدسية غولدباخ (بالإنجليزية: Goldbach's conjecture) هي حدسية اقترحها عالم الرياضيات الألماني كريستيان غولدباخ عام 1742. واحدة من أقدم المسائل غير المحلولة في نظرية الأعداد وفي الرياضيات ككل. وتنص على ما يلي:
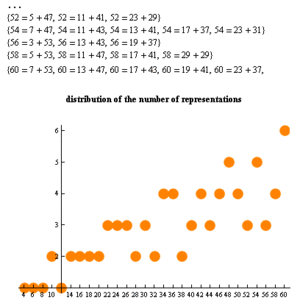
عدد الطرق المختلفة التي يكتب بها عدد زوجي ما أكبر قطعا من 2 على شكل مجموع عددين أوليين يسمى عدد غولدباخ.
تاريخ
عدلفي السابع من يوليو، عام 1742، كتب عالم الرياضيات ذو الأصل الألماني غولدباخ رسالة إلى أويلر جاء فيها:
- كل عدد زوجي أكبر من 6 يساوي حاصل مجموع عددين أوليين فرديين.
- كل عدد فردي أكبر من 9 يساوي حاصل مجموع ثلاثة أعداد أولية فردية.
وبشكل واضح الحدسية الثانية يمكن اشتقاقها من الأولى وذلك لأنه يمكن كتابة كل عدد فردي بالشكل التالي: ، وقد عبّر أويلر عن إيمانه بصحة هذه الحدسية ولكنه لم يستطع أن يقدم برهانا، وقد تم فحص هاتين الحدسيتين على مر السنين بالطرق العددية مثال: شين موك كونج فحص الحدسية حتى العدد وقد وصل كل من لايت وفوريس وهاموند وروي إلى وفي عام 1998 وصل الحد إلى .
وفي الخطاب المشهور في اجتماع كونغرس الرياضيات الذي أقيم في باريس عام 1900، أعلن هيلبرت 23 مسألة غير محلولة والتي يجب أن يعمل عليها الرياضياتيون في القرن ال-20 وقد تم ذكر هذه المسألة من ضمن المسائل، وفي عام 1912 أعلن لاندو عن أربعة مسائل في نظرية الأعداد الأولية من ضمنها حدسية غولدباخ والتي لا يوجد لها حل وذلك ضمن خطابه في اجتماع كونغرس الرياضيات الخامس والذي عقد في كامبريج. في عام 1921 أعلن هاردي في خطابه أمام المجتمع الرياضياتي في كوبنهاغن أن المسألة ليست فقط من أصعب المسائل في نظرية الأعداد ولكن في كل الرياضيات.
وفي عشرينيات القرن العشرين حدث تقدم ملحوظ على المسألة حيث أن قبلها لم تكن هناك وسائل البتة لحل المسألة وقد تركز البحث على فحص الأعداد أوفي بعض الأحيان كتابة حدسيات جديدة مشتقة من الحدسية. وقد كانت الوسيلة الجديدة تسمى «طريقة الدائرة» وقد استخدمها الرياضياتيان هاردي وليتل-وود في عام 1923 أن كل عدد فردي كبير هو مجموع ثلاثة أعداد أولية فردية وتقريبا كل عدد زوجي هو مجموع عددين أوليين فرديين وتم ذلك بافتراض أن حدسية ريمان الموسعة صحيحة. وقد كان الرياضياتي النرويجي برون بواسطة وسيلة الغربال عام 1919 قد توصّل إلى أن كل عدد زوجي كبير هو مجموع عددين بحيث أن كل منها يمكن تفكيكه ل-9 عوامل أولية على الأكثر، وفي 1930 نجح العالم الروسي لييف شنايرلمان بالتوصل إلى نظرية مهمة في نظرية الأعداد المتطرقة إلى المجاميع وهي: يوجد عدد c صحيح حيث كل عدد صحيح أكبر من 2 هو مجموع c أعداد أولية على الأكثر.
وفي عام 1937 نجح العالم الروسي فينوغرادوف في إزالة العلاقة مع نظرية ريمان الموسعة وذلك بواسطة «طريقة الدائرة» وأيضا بواسطة طريقته المبتكرة لتقريب المجموع الأسي على الأعداد الاولية (وهو ) ونجح ببرهنة ما تم سابقا بواسطة ليتيل-وود وهاردي ولكن دون الحاجة لنظريات ريمان.
وبعد تطورات عديدة على «وسيلة الغربال» التي طورها برون نجح العالم الصيني تشين جن رن في عام 1966 نجح بالتوصل إلى أن كل عدد زوجي هو مجموع عدد أولي وعدد آخر لديه عاملان أوليان على الأكثر.
في عام 1995 نجح راميري ببرهنة نظرية أضعف من حدسية غولدباخ وهي تنص على أن كل عدد زوجي يمكن كتابته بشكل مجموع ستة أعداد أولية على الأكثر. وفي نفس العام نجح كانيكي بالتوصل لنظرية اقوى: إذا افترضنا نظرية ريمان حينها كل عدد زوجي يمكن كتابته بشكل مجموع خمسة أعداد أولية على الأكثر. ويمكن تقوية نظرية كانيكي للوصول حتى أربعة أعداد أولية بربطها مع مسألة فحص حسابية.
مسائل معممة
عدليمكن تعميم حدسية غولدباخ بشكل يسمح بدراسة مسألة أكثر شمولية بحيث هذه المسألة يمكن أن يتفرع منها مسائل أخرى هي أيضا مهمة:
مسألة 1: فلتكن مجموعة جزئية ل- وليكن عدد صحيح، ما هي المجموعة: .
مسألة 2: فلتكن مجموعة جزئية ل- ، ما هي المجموعة: .
يمكن اشتقاق مسائل مهمة من هذه المسائل وهي كالتالي:
- حدسية غولدباخ: إذا اخترنا أي أننا اخترنا مجموعة الأعداد الأولية الموجبة واخترنا حينها المسألة 1 تكون كالتالي: والتي حسب حدسية غولدباخ تضم كل الأعداد الزوجية أكبر من 2.
- نظرية فينوجرادوف: إذا اخترنا أي أننا اخترنا مجموعة الأعداد الأولية الموجبة واخترنا حينها المسألة 1 تكون كالتالي: وهي تضم حسب نظرية فينوجرادوف كل الأعداد الفردية الكبيرة كفاية.
طور العلمان هاردي وليتل-وود طريقة الدائرة للتعامل مع هذا النوع من المسائل وقد لاقت هذه الطريقة نجاحا باهرا حيث تم برهنة نظرية فينوجرادوف إذ أنها تعتبر تقدم هائل نحو برهنة الحدسية وذلك للتقارب بينهما.
طريقة الدائرة
عدلهاردي وليتل وود (1921) في الأصل استخدما الطريقة لحلّ مسألة كتابة الأعداد الصحيحة بشكل مجموع أعداد صحيحة مرفوعة بالقوة k. لنفرض أن عدد الطرق لكتابة n بواسطة d أعداد صحيحة مرفوعة بالقوة k. وهذه الطريقة هي لتقريب قيمة عندما و- k كبير جدا بالنسبة ل-d.
الفكرة العامة لهذه الطريقة هي كالتالي: ل- عرف الدالة المنتجة التالية:
ولاحظ أن معامل في الدالة هو عدد طرق طرق كتابة بشكل حاصل جمع أعداد من المجموعة . ولكن من جهة أخرى هذا المعامل هو:
وبواسطة صيغة كوشي التكاملية:
حيث أن منحنى طوله نهائي. والفكرة هي إيجاد طريقة بديلة لحساب التكامل وذلك لتقريب قيمة . وعندما يكون المنحنى دائري التكامل يمكن اختصاره لتكامل مجاميع أسية وهي الطريقة التي استخدمها فينوجرادوف عام 1929.
أمثلة
عدل- 4=2+2
- 6=3+3
- 8=3+5
- 10=5+5=3+7
- 12=5+7
- 14=7+7=3+11
- 16=5+11=3+13
- 18=7+11=5+13
- 20=3+17=7+13
- 22=3+19=5+17
- 24=5+19=7+17
- 26=7+19=13+13
نتائج متحقق منها
عدللقد تم فحص حدسية غولدباخ لإيجاد مثال مضاد ولكن عبثا إذ أن ديسبوفيس (1855) فحص الحدسية لكل عدد أصغر من 10,000، وفي عام 1940 فحص بيبينغ الحدسية حتى العدد 100,000 بواسطة الحاسوب وعام 1964 بواسطة العالمين ستين وستين وصل الفحص حتى العدد وفي الأعوام التي تلت نجح جرانفيل ولون ورايلي بالوصول إلى وذلك كان عام 1989. وفي عام 1998 توصل ديشوليرس رايلي وساوتر بالوصول إلى أما ريتشستاين وصل بفحصه حتى: .
حدسيات مماثلة
عدل- حدسية غولدباخ الضعيفة: كل عدد فردي أكبر من 9 يساوي حاصل مجموع ثلاثة أعداد أولية فردية. وكما تم ذكر هذا سابقا فإنه يمكن اشتقاق هذه الحدسية من الأولى، وقد تم برهنة هذه الحدسية عام 2013 .
في الثقافة الشعبية
عدل- حتى يكتسب الكتاب Uncle Petros وحدسية غولدباخ الشهرة والذي كتبه أبوستولوس دوكسيادس، عرض الناشر البريطاني طوني فابر جائزة بقيمة 1000000 دولار لمن يبرهن الحدسية قبل أبريل 2002، الجائزة لم يحصل عليها أحد.
- وفي الدراما التلفزيونية "Lewis" حصل عالم رياضيات على جائزة فيلدز لعمله على حدسية غولدباخ.
- وفي القصة القصيرة لإسحاق إسيموف "Sixty Million Trillion Combinations" يذكر فيها أن عالم رياضيات شك أن أعماله على حدسية غولدباخ قد سُرقت.
- وفي الفلم الإسباني " (La habitación de Fermat (2007" أعلن رياضياتي شاب أنه وجد برهان الحدسية.
- وفي الكارتون «مغامرات جيمي نيوترون» قال جيمي في إحدى الحلقات أنه كان في وسط إيجاد برهان لحدسية غولدباخ.
- وفي الفيلم "(The Calculus of Love (2011" كان هناك أستاذ مهووس بإيجاد برهان للحدسية.
- وفي الفيلم الكوري "Perfect Number" أستاذ رياضيات كان مهووسا بإيجاد برهان للحدسية.
انظر أيضا
عدلمراجع
عدل- ^ “حدسية غولدباخ" by Hector Zenil, Wolfram Demonstrations Project, 2007. نسخة محفوظة 03 يونيو 2018 على موقع واي باك مشين.
| في كومنز صور وملفات عن: حدسية غولدباخ |