قوانين مساحة المثلث
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. (مارس 2016) |
في الهندسة الرياضية، تعطى مساحة المثلث بالقانون:
المساحة = ½×طول القاعدة × الارتفاع
يقصد بالقاعدة أحد أضلاع المثلث ويقصد بالارتفاع العمود النازل من الرأس على القاعدة أو على امتدادها.
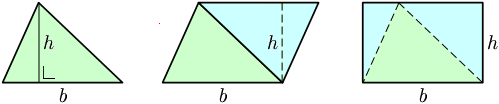
لاثبات ما سبق يحول المثلث إلى متوازي أضلاع مساحته ضعف مساحة المثلث،
و بعدها يحول إلى مستطيل طوله قاعدة المثلث وعرضه ارتفاع المثلث.
و من هذا القانون تستنتج قوانين مساحة المثلث الأخرى.
قوانين المساحة للمثلث عدل
القانون الأول عدل
يربط بين مساحة المثلث وبين جيب إحدى زواياه.
في المثلث ABC: القطعة المستقيمة AN ارتفاع و a,b,c أطوال أضلاع المثلث.
المثلث ANC مثلث قائم في N:
(جيب الزاوية يساوي المقابل على الوتر في المثلث القائم)
القانون الثاني عدل
يوضح علاقة مساحة المثلث بنصف قطر الدائرة المحيطة به R.
البرهان:
باستخدام قانون الجيوب:
القانون الثالث عدل
يربط بين مساحة المثلث و نصف قطر الدائرة الداخلية r و نصف المحيط s.
البرهان:
P مركز الدائرة الداخلية للمثلث
باستخدام «المساحة = ½ القاعدة × الارتفاع» ثلاث مرات:
القانون الرابع عدل
يعرف بصيغة هيرو:
باعتبار أن a,b,c اطوال اضلاع المثلث قيم معلومة، فإن مساحة المثلث هي:
حيث أن s نصف محيط المثلث.
القانون الخامس عدل
يعرف بصيغة جيوشاو:
القانون السادس عدل
مساحة المثلث القائم بدلالة طول الوتر والمحيط تُعطى بالعلاقة: المساحة = (1 / 4) [ (المحيط)^2 - 2 × المحيط × طول الوتر ]