سرعة زاوية
في الفيزياء، السرعة الزاوية هي متجهة التي تعبر عن التردد الزاوي والمحور الذي يدور حوله الجسم.[1][2][3] وحدة قياس السرعة الزاوية في نظام الوحدات الدولي هي الراديان/ثانية ، ومن الممكن قياسها بواحدات أخرى مثل درجة في الثانية. عندما تُقاس بوحدة دورة في وحدة الزمن (دورة في الدقيقة، أو دورة في الساعة...الخ) فإنه يطلق عليها اسم السرعة الدورانية.
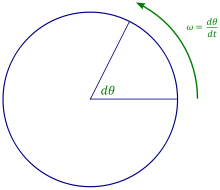
يُرمز للسرعة الزاوية بالحرف أوميغا (Ω أو ω). جهة متجهة السرعة الزاوية تكون عمودية على مستوي الدوران، والتي تـُحدد غالباً باستخدام قاعدة اليد اليمنى.
الصيغة الرياضية
عدلنفترض حالة حركة دائرية فتكون السرعة الزاوية' ، أي معدل تغير الزاوية مع الزمن :
ومنه نحصل على زمن الدورة T الواحدة :
وتبلغ سرعة نقطة على دائرة دوران ذات نصف قطر :
ويبلغ عدد الدورات في الثانية :
في الحركة الاهتزازية يمثل التردد عدد الاهتازات الكاملة (الدورات) في وحدة الزمن. وفي كل دورة يتغير مسقط المطال طبقا لدالة جيبية ويعبر زاوية قدرها .
من ذلك يمكننا حساب التردد الزاوي :
وتناظر صيغة التردد صيغة عدد الدورات :
هذه المعادلة تبين العلاقة بين التردد f والسرعة الزاوية . ويقاس التردد هرتز أو 1/ثانية، أما السرعة الزاوية فهي تقاس ب راديان/ثانية.
| الرموز الشائعة |
ω |
|---|---|
| التعريف الرياضي | |
| نظام الوحدات الدولي | |
| شمولية ؟ |
yes |
| مكثفة ؟ |
yes (for rigid body only) |
| الاشتقاق من كميات أخرى |
ω = dθ / dt |
| التحليل البعدي |
موتر
عدلمتجهة السرعة الزاوية يمكن التعبير عنها بالتساوي على أنها موتر (Tensor) السرعة الزاوية، المصفوفة (أو الخريطة الخطية) (W = W(t تعطى على الشكل التالي:
- هذه مصفوفة دوران متناهية الصغر. المصفوفة W تتصرف ك :
الحساب من مصفوفة الاتجاه
عدلالخضوع لحركة دائرية منتظمة حول محور ثابت يستوفي:
بالنظر إلى مصفوفة التوجه (A(t لإطار، أعمدتها هي متجهات متعامدة متحركة ذات إحداثيات ، يمكننا الحصول على موتر السرعة الزاوية (W(t كالتالي: يجب أن تكون السرعة الزاوية هي نفسها بالنسبة إلى المتجهات الثلاثة لذلك بعد ترتيب المعادلات المتجهية الثلاثة في أعمدة مصفوفة، لدينا:
(هذا حتى لو (A(t لا تدور بشكل موحد). لذلك موتر السرعة الزاوية هو:
بحيث معكوس المصفوفة المتعامدة، هو منقولها .
خصائص
عدلعامة، السرعة الزاوية في فضاء ذو أبعاد n) n: عدد الأبعاد) هو المشتق الزمني لموتّر الإزاحة الزاوية، وهو موتر متماثل منحرف من المرتبة الثانية.
هذا الموتر W سيكون لديه n(n−1)/2 عناصر مستقلة، وهو بُعد جبر لي (Lie Algebra) من مجموعة لي (Lie Group) ذات تناوب مساحة المنتج الداخلية ذات الأبعاد n.[6]
الازدواجية فيما يتعلق بمتجهة السرعة
عدلفي ثلاثة أبعاد، السرعة الزاوية يمكن تمثيلها بواسطة متجهة زائفة (pseudovector) لأن الموترات من الرتبة الثانية مزدوجة بالنسبة إلى المتجهات الزائفة (pseudovectors ) في ثلاثة أبعاد. حيث أن متوتر السرعة الزاوية (W=W(t عبارة عن مصفوفة منحرفة متماثلة:
إنها مزدوجة هودج وهي متجهة، وهي بالضبط متجهة السرعة الزاوية السابقة
أُسية W
عدلإذا عرفنا الإطار الأولي (A(0 ولدينا سرعة موتر زاوية ثابتة W، يمكننا الحصول على (A(t لأي زمن t. نذكر معادلة المصفوفة التفاضلية:
يمكن حساب تكامل هذه المعادلة لتعطينا:
مما يدل على وجود صلة مع مجموعة لي من الدورات.
W منحرف متماثل
عدلنثبت أن موتر السرعة الزاوية هو انحراف متماثل، يعني لتعطينا .
إن مصفوفة الدوران A متعامدة، عكس منقولها، إذا لدينا . لكل إطار مصفوفة . إزالة مشتق الزمن من المعادلة يعطينا:
.
بتطبيق المعادلة .
.
وبالتالي W هو سلبي بالنسبة لمنقوله ، مما يعني أنه منحرف متماثل.
وصف خالٍ من الإحداثيات
عدلفي أي لحظة t، موتر السرعة الزاوية يمثل خريطة خطية بين موضع المتجهة (r(t وسرعة المتجهات (v(t لنقطة على جسم صلب تدور حول الأصل: العلاقة بين هذه الخريطة الخطية ومتجهة السرعة الزاوية الزائفة هي كالتالي.
لأن w هو مشتق التحول المتعامد (orthogonal transformation)، الشكل الخطي:
هو منحرف متماثل. وبالتالي يمكننا تطبيق حقيقة الجبر الخارجي بأن هناك شكلًا خطيًا فريدًا ل حيث:
حيث أن هو الناتج الخارجي ل و
نأخذ ♯L لـ L تعطينا:
نعطي ، كمزدوجة هودج (Hodge dual) لـ ♯L وبتطبيق تعريف مزدوجة هودج مرتين بافتراض أن الوحدة المفضلة ل 3 متجهات هو
بحيث: حسب التعريف.
لأن متجهة اختيارية، من عدم انحلال للجداء العددي بالتالي:
السرعة الزاوية كمجال متجهي
عدلبما أن موتر سرعة الدوران الزاوية لجسم صلب (في إطارها الإفتراضي). هو تحويل خطي يضع المواضع على السرعات (داخل الجسم الصلب)، يمكن اعتبارها مجال متجهي ثابت، على وجه الخصوص ، السرعة الزاوية لللف (الغزل) هي مجال متجهي قاتل ينتمي إلى عنصر من عناصر جبر لي (SO(3 لمجموعة الدوران ثلاثية الأبعاد (SO(3.
أيضًا ، يمكن إثبات أن المجال المتجهي للسرعة الزاوية الدورانية هو بالضبط نصف دوران مجال متجه السرعة الخطية (v(r لجسم صلب، بالأرقام:
انظر أيضًا
عدلمراجع
عدل- ^ K.S.HEDRIH: Leonhard Euler (1707–1783) and rigid body dynamics نسخة محفوظة 06 ديسمبر 2016 على موقع واي باك مشين.
- ^ Hibbeler، Russell C. (2009). Engineering Mechanics. Upper Saddle River, New Jersey: Pearson Prentice Hall. ص. 314, 153. ISBN:978-0-13-607791-6. مؤرشف من الأصل في 2019-12-08.
- ^ "online tool to calculate angular speed vectors". Aeroengineering.info. مؤرشف من الأصل في 2016-03-05. اطلع عليه بتاريخ 2013-01-23.
- ^ Quantities and units — Part 3: Space and time (بالإنجليزية والفرنسية) (2nd ed.), International Organization for Standardization, 2019-10, 3-12, QID:Q90137277
{{استشهاد}}: تحقق من التاريخ في:|publication-date=(help) - ^ Quantities and units—Part 3: Space and time (بالإنجليزية) (1st ed.), International Organization for Standardization, 1 Mar 2006, 3-10.a, QID:Q26711932
- ^ Rotations and Angular Momentum on the Classical Mechanics page of the website of John Baez, especially Questions 1 and 2. نسخة محفوظة 2020-11-25 على موقع واي باك مشين.
| في كومنز صور وملفات عن: سرعة زاوية |