الإبدال بالإزاحة الدنيا
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. (يناير 2022) |
الإبدال بالإزاحة الدنيا (بالإنجليزية: Minimum Shift Keying اختصاراً MSK) وهي طريقة مطورة عن الإبدال بإزاحة التردد مع التقليل من التغيير المفاجئ للتردد والشكل. في هذه الطريقة تفصل المعلومات الرقمية إلى معلومات زوجية even bits ومعلومات فردية odd bits وتتم مضاعفة الفترة الزمنية لكل معلومة رقمية. ويستخدم قيمتان تردديتان وهي التردد المنخفض f1 والتردد العالي f2 وتكون f2=2*f1. ويتم اختيار أحد الترددين حسب ما يلي:
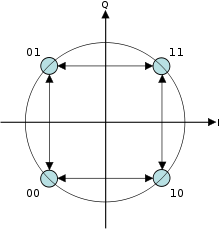
إذا كان كل من المعلومة الزوجية والفردية في حالة 0 يتم استخدام التردد العالي f2 ومع عكس الموجة (تغيير في زاوية الطور بمقدار 180°) إذا كانت المعلومة الزوجية في حالة 1 والمعلومة الفردية في حالة 0 يتم استخدام التردد المنخفض f2 ومع عكس الموجة (تغيير في زاوية الطور بمقدار 180°) إذا كانت المعلومة الزوجية في حالة 0 والمعلومة الفردية في حالة 1 يتم استخددام التردد المنخفض f2 دون تغيير زاوية الطور إذا كان كل من المعلومة الزوجية والفردية في حالة 1 يتم استخدام التردد العالي دون تغيير زاوية الطور وبإضافة مرشح منخفض جاوسي Gaussian law-pass filter إلى معدل الإزاحة الدنيا نحصل على ما يسمى معدل الإزاحة الدنيا الجاوسي Gaussian Minimum Shift Keying GMSK. وهو المعدل المستخدم في أنظمة الاتصالات اللاسلكية الأوروبية جي إس إم و DECT.
التعبير الرياضي
عدلالإشارة الناتجة يمكن التعبير بيها بالمعادلة الرياضية التالية :
خطأ رياضيات (خطأ في الصياغة): {\displaystyle s(t) = a_{I}(t)\cos{\left(\frac{{\pi}t}{2T}\right)}\cos{(2{\pi}f_{c}t)}-a_{Q}(t)\sin{\left(\frac{{\pi}t}{2T} ight)}\sin{\left(2{\pi}f_{c}t ight)}}
حيث و يقومان بتشفير المعلومات الفردية و الزوجية بترتيب أو تسلسل نبضات رباعية بفترة تساوي 2T. باستعمال قائمة المطابقات المثلثية يمكن لهذه المعادلة أن تتم إعادة كتابتها في صيغة بحيث طورو تردد التضمين يكونان واضحين أكثر كالتالي :
حيث bk(t) هي +1 عندما و -1 إذا كانا من إشارات مختلفة و is 0 if is 1, and otherwise. Therefore, the signal is modulated in frequency and phase, and the phase continuously and linearly changes.
المصادر
عدل- Subbarayan Pasupathy, Minimum Shift Keying: A Spectrally Efficient Modulation, IEEE Communications Magazine, 1979
- Document from the University of Hull giving a thorough description of GMSK.
- Another good discussion (University of Toronto)
- PSK/GMSK comparison & illustrations (Aerospace)