مخطط مستو
في المخططات، المخطّط المستوي هو المخطّط الذي يقبل تمثيلا في المستوى، بحيث لا يتقاطع أي حرفين من المخطّط.[1][2][3]
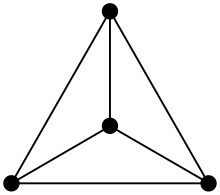
معايير المخطّط المستوي
عدلحسب كوراتوفسكي, يكون المخطط مستويا إذا لم يتضمن زمرة من الرتبة الخامسة، أو مخططا ثنائيا كاملا من الرتبة الثالثة.
وجوه مخطط مستوي
عدلليكن G مخططا مستويا، الوجه F هو أكبر منطقة من المستوى محدّدة بمجموعة حروف G ولا تتضمن أيا منها.
ليكن G مخطّطا مستويا، و a عدد حروف G. إذن :
صيغة أويلر
عدلتعاريف
عدل- المسار ذو الطول r هو سلسلة من القمم المرتبطة مع أصل السبيل و طرفه.
- يكون المخطّط متّصلا إذا وُجد مسار بين كل قمتين من G.
- المسار المغلق هو حالة .
- الشجرة هي مخطط متّصل بدون أي مسار مغلق.
تمهيدة
عدلكل مخطّط متّصل يمكن الحصول عليه بإضافة عدّة قمم لشجرة (لها نفس عدد القمم).
صيغة أويلر للمخطّطات المستوية المتّصلة
عدلليكن G مخطّط مستوي متّصل. ليكن n عدد قمم a, G عدد حروفه و f عدد وجوهه. إذن: n − a + f = 2
المعايير
عدلتحديد المعايير التي تمكّن من معرفة ان كان مخطّط ما مستويا. ليكن G مخطّط مستوي متّصل. ليكن n عدد قمم a, G عدد حروفه:
- في حالة وجود مثلّثات.
- في حالة عدم وجود مثلّثات.
مميّزة كوراتوفسكي
عدلالرياضي البولوني كوراتوفسكي وضع الميّزة التالية للمخطّطات المستوية :
- يكون المخطّط مستويا إذا وفقط إذا لم يتضمّن مخطّطا جزئيّا عبارة عن تمديد ل K5 (زمرة ب 5 قمم) أو K3,3 (المخطّط ثنائي كامل ب3+3 رؤوس).
'التمديد بالنّسبة لمخطّط هو نتيجة إضافة قـمّة أو أكثر لحرف أو عدّة حروف (مثلا، تحويل الحرف•——• إلى •—•—•).
انظر أيضًا
عدلمراجع
عدل- ^ Trudeau، Richard J. (1993). Introduction to Graph Theory (ط. Corrected, enlarged republication.). New York: Dover Pub. ص. 64. ISBN:978-0-486-67870-2. مؤرشف من الأصل في 2019-05-05. اطلع عليه بتاريخ 2012-08-08.
Thus a planar graph, when drawn on a flat surface, either has no edge-crossings or can be redrawn without them.
- ^ Bonichon، N.؛ Gavoille، C.؛ Hanusse، N.؛ Poulalhon، D.؛ Schaeffer، G. (2006). "Planar Graphs, via Well-Orderly Maps and Trees". Graphs and Combinatorics. ج. 22: 185–202. CiteSeerX:10.1.1.106.7456. DOI:10.1007/s00373-006-0647-2.
- ^ Giménez، Omer؛ Noy، Marc (2009). "Asymptotic enumeration and limit laws of planar graphs". Journal of the American Mathematical Society. ج. 22: 309–329. arXiv:math/0501269. DOI:10.1090/s0894-0347-08-00624-3.
| في كومنز صور وملفات عن: مخطط مستو |